Concentration (shown on the vertical axis of the plot) is typically normalized to the initial concentration injected into media and the time (on the horizontal axis) is often nondimensionalized by presenting it as the number of pore volumes (PV) entered the system. A range of underlying mechanisms of material transport in porous media may be inferred from the shape of the breakthrough curve.

Inferring transport characteristics from the shape of breakthrough curves 

The shape of breakthrough curves may be used to deduce different underlying transport mechanisms for solutes and particles. This has especially become important for nanoparticle transport studies in recent years as there is a range of mechanisms that simultaneously affect the transport of these materials and having a knowledge of how these mechanisms change the shape of BTC may help to identify the underlying transport mechanisms This helps to select the right model for simulating the transport of materials in porous media (Babakhani et al., 2017). 

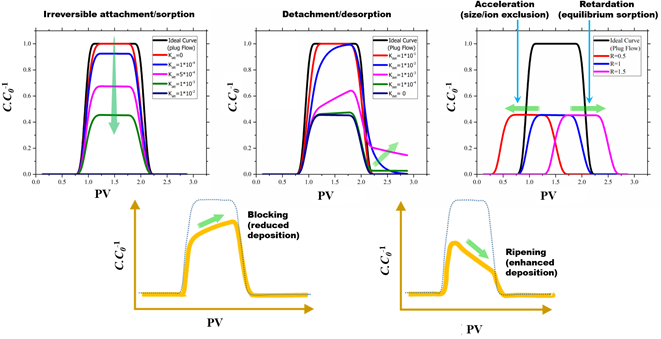
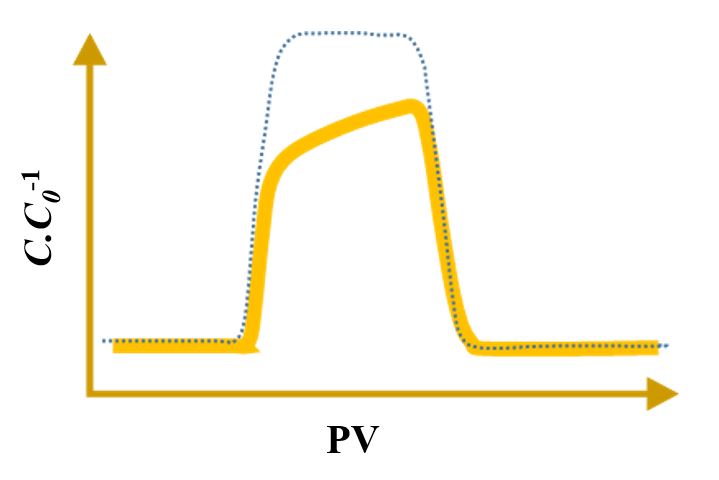
Compared to a standard conservative BTC which look like a rectangular, a round-shaped BTC which is broader at the bottom and narrower at the top generally represents a dispersive transport behaviour rather than advective. A BTC with tailing indicates detachment of retained particle or desorption of adsorbed solute during the flushing phase of single- or multi-pulse BTC. An ascending plateau of BTC signifies blocking of attachment or adsorption sites in porous media by one layer of particles or solute ions/molecules/macromolecules/polymers and thus facilitating the transport of subsequent materials entering the system. A descending plateau observed for colloidal particles and nanoparticles may point to the ripening mechanism which, in contrast to the blocking mechanism, results from further retention of subsequent particles following the deposition of initial particles. In other words, the retention of particles initially entered the system, provide more deposition sites for subsequent particles entering the system and thus the retention process is progressive with time in a BTC with an ascending plateau. 

A total reduction in the area under the BTC may indicate the irreversible retention or sorption of colloidal particles/nanoparticles or solutes, respectively. If the plateau of BTC is flat, the deposition mechanism may result from physicochemical deposition, i.e., deep interaction energy minima. This may also be a concomitant process with particle aggregation inside pores since the growth in aggregate sizes leads to deeper energy wells (Babakhani, 2019; Babakhani et al., 2018; Phenrat et al., 2009). A horizontal shift in BTC towards later times (retardation) results from equilibrium adsorption (which is mainly a solute transport behaviour) while a shift towards earlier times (accelerated BTC) may emanate from size exclusion (a particle transport behaviour) or charge exclusion (a solute transport behaviour) (Babakhani, 2019; Babakhani et al., 2017; Van Genuchten, 1981). 

Different shapes of a single-pulse breakthrough curve representing specific mechanisms of solute or particle transport in porous media. 

Number of pore volumes on the time axis of breakthrough curves

The horizontal axis of the breakthrough curve, which shows the time elapsed, is often presented as a dimensionless number called pore volume or the number of pore volumes (PV) [–] determined as: 

 PV = Q.t/Vv,

where Q is the flow rate [L3.T-1], t is the time elapsed [T], and Vv is the total volume of voids in the system and can be determined by multiplying the total volume of the system by the porosity of the porous medium. For cylindrical column experiments, which aims to mimic one-dimensional transport of materials, Vv is: 

Vv=φ.π.rc2.Lc,

where φ is the porosity of the porous medium [–], rc is the inner radius of the column [L], and Lc is the length of the column [L]. Using the continuity equation, PV can be determined as: 

PV = v.t/Lc, 

where v is the pore water velocity (also known as real water velocity, linear groundwater flow velocity, seepage water velocity, interstitial velocity, or advection velocity) [L.T-1], which is equal to porosity times the Darcy velocity (also known as the superficial velocity or approach velocity). 

Continuous, single-pulse, and multi-pulse injection 

If the duration of material injection is shorter than the monitoring period and the return towards the base-flow condition is observed in the effluent sample concentrations, the resultant BTC appears as a single- or multi-pulse curve, otherwise, it appears as a continuous curve. Single- or multi-pulse breakthrough curves give additional information about the desorption or detachment processes of materials based on the shape of descending limb of the curve that is overlooked in continuous injection (Mahmoudi et al., 2020). Multi-pulse breakthrough curves are mostly products of the step-wise changes in the condition of injected materials or background flow, e.g., changing the ionic strengths or pH, aimed at evaluating their variations in a single experiment (Torkzaban et al., 2010). If the flow condition (e.g., pore water velocity) is changed across different pulses, using a zero velocity should be avoided since it will result in no effluent samples during that period, and consequently zero pore volume on the horizontal axis of the breakthrough curve thereby ignoring the processes that may happen during the stop-flow period and afterwards. 

Multi-peak or multi-shoulder BTC may appear for single- or multi-pulse BTC, because of heterogeneity in the packed media, e.g., in a stratigraphic, heterogeneous packed tank, material plumes from different layers may arrive at the outlet at different times and thus appear as multiple peaks in BTC (Babakhani et al., 2018; Phenrat et al., 2010).